Eller: hvordan unngå Polynom Lang Divisjon når finne faktorer
husker du å gjøre divisjon I Aritmetikk?
«7 dividert med 2 er lik 3 med en rest på 1»
hver del av divisjonen har navn:

Som kan skrives om som en sum som dette:
Polynomer
Vel, vi kan også dele polynomer.
f (x) ÷ d (x) = q (x) med en rest på r (x)
Men det er bedre å skrive det som en sum som dette:
Som i dette eksemplet ved Hjelp Av Polynom Lang Divisjon:
Eksempel: 2×2−5x-1 delt på x−3
- f (x) er 2×2-5x-1
- d(x) er x−3
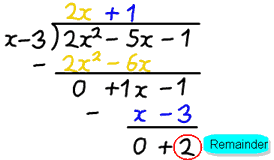
etter deling får vi svaret 2x + 1, men det er en rest på 2.
- q (x) er 2x + 1
- r(x) er 2
i stilen f (x) = d (x) * q (x) + r (x) kan vi skrive:
2×2-5x-1 = (x−3) (2x+1) + 2
Men du trenger å vite en ting til:
graden av r (x) er alltid mindre enn d (x)
Si at vi deler med et polynom av grad 1 (som» x−3″) resten vil ha grad 0 (med andre ord en konstant, som»4″).
Vi vil bruke den ideen i «Rest Theorem»:
Rest Theorem
når vi deler f (x) med det enkle polynomet x-c får vi:
f (x) = (x−c)·q(x) + r(x)
x−c er grad 1, så r(x) må ha grad 0, så det er bare noen konstant r :
f (x) = (x−c)·q (x) + r
se nå hva som skjer når vi har x lik c:
så vi får dette:
Resten Teoremet:
når vi deler et polynom f (x) med x-c resten er f (c)
Så for å finne resten etter å ha delt med x-c trenger vi ikke å gjøre noen divisjon:
bare beregne f (c).
La oss se det i praksis:
Eksempel: resten etter 2×2-5x – 1 er delt med x−3
(vårt eksempel ovenfra)
vi trenger ikke å dele med (x−3) … bare beregne f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
og det er resten vi fikk fra våre beregninger ovenfor.
Vi trengte ikke Å Gjøre Lang Divisjon i Det hele tatt!
Eksempel: Resten etter 2×2-5x – 1 er delt med x−5
Samme eksempel som ovenfor, men denne gangen deler vi med «x−5»
«c» er 5, så la oss sjekke f(5):
2(5)2-5(5)-1 = 2×25-5×5−1
= 50-25-1
= 24
resten er 24
Igjen … Vi trengte ikke Å Gjøre Lang Divisjon for å finne det.
Faktorteoremet
Nå …
Hva om vi beregner f (c) og det er 0?
… det betyr at resten er 0, ja …
… (x-c) må være en faktor av polynomet!
vi ser dette når vi deler hele tall. For eksempel 60 ÷ 20 = 3 uten rest. Så 20 må være en faktor på 60.
Eksempel: x2−3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
så (x−4) må være en faktor på x2-3x−4
Og så har vi:
Faktorteoremet:
når f (c)=0 så er x-c en faktor av f (x)
og omvendt også:
når x-c er en faktor av f (x) så f (c)=0
Hvorfor Er Dette Nyttig?
Å Vite at x-c er en faktor er det samme som å vite at c er en rot(og omvendt).
faktoren «x-c» og roten «c» er det samme
Kjenner en og vi kjenner den andre
for en ting betyr det at vi raskt kan sjekke om (x-c) er en faktor av polynomet.
Eksempel: Finn faktorene til 2×3-x2-7x+2
polynomet er grad 3, og kan være vanskelig å løse. Så la oss plotte det først:
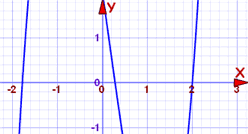
kurven krysser x-aksen på tre punkter, og en av dem kan være på 2. Vi kan sjekke enkelt:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Ja! f(2) = 0, så vi har funnet en rot og en faktor.
Så (x−2) må være en faktor på 2×3-x2-7x+2
Hva med hvor den krysser nær -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
nei, (x+1.8) er ikke en faktor. Vi kan prøve noen andre verdier i nærheten og kanskje få heldige.
Men i det minste vet vi (x−2) er en faktor, så la oss bruke Polynom Lang Divisjon:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
som forventet er resten null.
Enda Bedre, vi er igjen med den kvadratiske ligningen 2×2 + 3x – 1 som er lett å løse.
det er røtter er -1,78… og 0,28…, så det endelige resultatet er:
2×3−x2−7x+2 = (x−2)(x+1,78…) (x−0,28…)
Vi var i stand til å løse et vanskelig polynom.
Sammendrag
Resten Av Teoremet:
- når vi deler et polynom f (x) med x-c, er resten f (c)
Faktorteoremet:
- Når f (c) = 0 da x-c er en faktor av f (x)
- når x-c er en faktor av f(x) da f (c)=0


