Or: how to avoid Polynomial Long Division when finding factors
Do you remember doing division in Arithmetic?
“7 dividido por 2 é igual a 3, com um resto de 1”
Cada parte da divisão tem nomes:
o Que pode ser reescrita como uma soma, como este:
Polinômios
Bem, podemos também dividir polinômios.
f(x) ÷ d(x) = q(x) com um resto r(x)
Mas é melhor escrevê-lo como uma soma, como este:
Como neste exemplo usando o Polinômio de Divisão Longa:
Exemplo: 2×2−5x−1 dividido por x−3
- f(x) é 2×2−5x−1
- d(x) é x−3
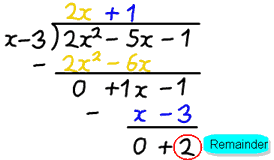
Após a divisão, podemos obter a resposta 2x+1, mas há um resto de 2.
- q(x) é 2x+1
- r(x) é 2
No estilo f(x) = d(x)·q(x) + r(x), podemos escrever:
2×2−5x−1 = (x−3)(2x+1) + 2
Mas você precisa saber mais uma coisa:
O grau de r(x) é sempre menor que d(x)
Dizer que dividir por um polinômio de grau 1 (tais como “x 3”) o remanescente terá o grau 0 (em outras palavras, uma constante, como “4”).
usaremos essa ideia no “Teorema do restante”:
o Teorema do restante
quando dividimos f(x) pelo polinômio simples x – C obtemos:
f(x) = (x−c)·q(x) + r(x)
x−c, grau 1, então r(x) tem grau 0, então é apenas alguns constante r :
f(x) = (x−c)·q(x) + r
ver Agora o que acontece quando temos x igual a c:
Então temos este:
O Restante Teorema:
Quando dividimos um polinˆ omio f(x) por x−c, o restante é f(c)
Então, para encontrar o resto depois da divisão por x-c nós não precisamos fazer qualquer divisão:
calcule f(c).
Vamos ver que, na prática,:
Exemplo: O resto depois de 2×2−5x−1 é dividido por x−3
(Nosso exemplo acima)
não precisamos dividir por (x−3) … basta calcular f(3):
2(3)2-5(3)-1 = 2×9−5×3−1
= 18-15-1
= 2
E que é o resto conseguimos com os nossos cálculos acima.Não precisávamos de fazer uma divisão longa!
exemplo: O resto depois de 2×2−5x−1 é dividido por x−5
o Mesmo exemplo acima, mas desta vez, dividimos por “x−5”
“c” é 5, então vamos verificar f(5):
2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24
O restante é de 24
mais uma Vez … Não precisávamos de fazer uma divisão longa para descobrir isso.
The Factor Theorem
Now …E se calcularmos f (C) e for 0?
… isso significa que o restante é 0, e …
… (x-C) deve ser um fator do polinômio!
vemos isto quando dividimos números inteiros. Por exemplo, 60 ÷ 20 = 3 sem resto. Então 20 deve ser um fator de 60.
Exemplo: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
assim, (x−4) deve ser um fator de x2−3x−4
E assim temos:
O Fator Teorema:
Quando f(c)=0, x−c é um fator de f(x)
E o contrário também:
Quando x−c é um fator de f(x), então f(c)=0
Por que Isso É Útil?
saber que x-c é um fator é o mesmo que saber que c é uma raiz (e vice-versa).
O fator “x−c” e a raiz “c” são a mesma coisa
Sei, e nós sabemos que o outro
Para uma coisa, isso significa que podemos rapidamente verificar se (x−c) é um fator do polinômio.
exemplo: Encontre os fatores de 2×3-x2-7x + 2
o polinômio é grau 3, e pode ser difícil de resolver. Então, vamos planeá-lo primeiro.:
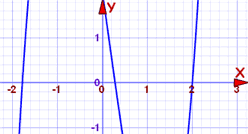
a curva atravessa o eixo x em três pontos, e um deles pode estar em 2. Podemos verificar facilmente:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Sim! f(2) = 0, então encontramos uma raiz e um fator.
So (x-2) deve ser um factor de 2×3-x2-7x+2
que tal onde passa perto de -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Não, (x+1.8) não é um fator. Podíamos tentar outros valores perto e talvez ter sorte.
Mas pelo menos sabemos que (x−2) é um fator importante, por isso vamos usar o Polinômio de Divisão Longa:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
Como esperado, o restante é zero. Melhor ainda, ficamos com a equação quadrática 2×2+3x – 1, que é fácil de resolver.
suas raízes são -1.78… e 0,28…, então o resultado final é:
2×3-x2-7x+2 = (x-2) (x+1, 78…) (x-0, 28…)
nós fomos capazes de resolver um polinômio difícil.
Resumo
O Restante Teorema:
- Quando dividimos um polinˆ omio f(x) por x−c, o restante é f(c)
O Fator Teorema:
- Quando f(c)=0, x−c é um fator de f(x)
- Quando x−c é um fator de f(x), então f(c)=0



