Area tröghetsmoment eller tröghetsmoment för ett område – även känd som andra Moment i området – I, är en egenskap av form som används för att förutsäga böjning, böjning och spänning i balkar.
- Area tröghetsmoment – Imperial enheter
- Area tröghetsmoment – metriska enheter
- konvertera mellan enheter
- exempel – konvertera mellan området tröghetsmoment enheter
- tröghetsmoment (tröghetsmoment för ett område eller ett andra Områdesmoment)
- Area tröghetsmoment för typiska tvärsnitt i
- fast kvadrattvärsnitt
- fast rektangulärt tvärsnitt
- fast cirkulärt tvärsnitt
- ihåligt cylindriskt tvärsnitt
- kvadratisk sektion – Diagonala Moment
- rektangulär sektion-Områdesmoment på vilken linje som helst genom tyngdpunkten
- symmetrisk form
- Nonsymmetrisk form
- Area tröghetsmoment vs. polärt tröghetsmoment vs. Tröghetsmoment
- sektionsmodul
Area tröghetsmoment – Imperial enheter
- tumes4
Area tröghetsmoment – metriska enheter
- mm4
- cm4
- m4
konvertera mellan enheter
- 1 cm4 = 10-8 m4 = 104 mm4
- 1 tum4 = 4, 16×105 mm4 = 41.6 cm4
exempel – konvertera mellan området tröghetsmoment enheter
9240 cm4 kan konverteras till mm4 genom att multiplicera med 104
(9240 cm4) 104 = 9.24 107 mm4
tröghetsmoment (tröghetsmoment för ett område eller ett andra Områdesmoment)
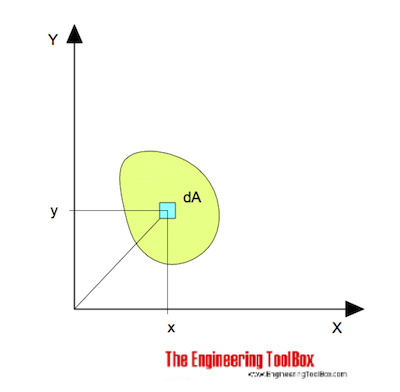
för böjning runt x-axeln kan uttryckas som
Ix = ätbar y2 dA (1)
där
Ix = Area tröghetsmoment relaterat till X-axeln (m4, mm4, inches4)
y = det vinkelräta avståndet från axel X till elementet da (m, mm, tum)
dA = ett elementärt område (m2, mm2, tum2)
tröghetsmomentet för böjning runt Y – axeln kan uttryckas som
Iy = x2 da (2)
där
Iy = Area tröghetsmoment relaterat till Y-axeln (M4, mm4, inches4)
x = det vinkelräta avståndet från axeln y till elementet dA (m, mm, inches)
Area tröghetsmoment för typiska tvärsnitt i
- Area tröghetsmoment för typiska tvärsnitt II
fast kvadrattvärsnitt
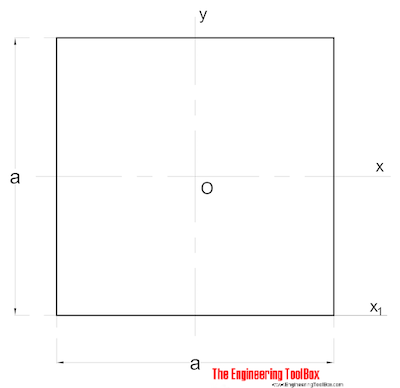
area tröghetsmoment för en fast kvadratisk sektion kan beräknas som
IX = a4 / 12 (2)
där
A = sida (mm, m, in..)
IY = a4 / 12 (2b)
fast rektangulärt tvärsnitt
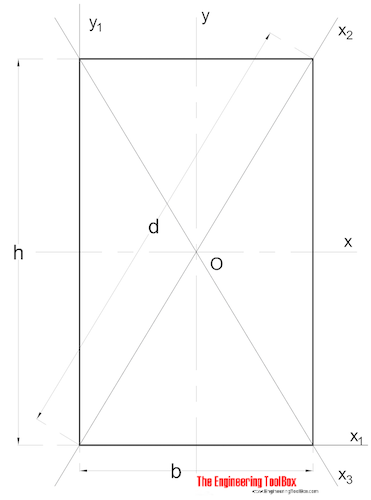
Areamomentet för Ineria för en rektangulär sektion kan beräknas som
Ix = B h3 / 12 (3)
där
b = bredd
h = höjd
Iy = b3 h / 12 (3b)
fast cirkulärt tvärsnitt
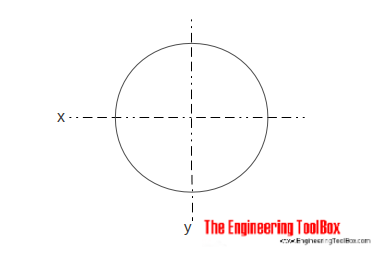
Area tröghetsmoment för en fast cylindrisk sektion kan beräknas som
Ix = r4 / 4
= Kubi d4 / 64 (4)
där
r = radie
d = diameter
IY = oc r4 / 4
= oc D4 / 64 (4b)
ihåligt cylindriskt tvärsnitt
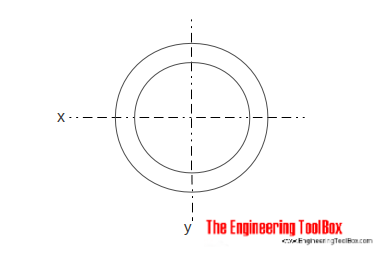
Area tröghetsmoment för en ihålig cylindrisk sektion kan beräknas som
Ix = oc (do4-di4) / 64 (5)
där
do = cylinder ytterdiameter
di = cylinder innerdiameter
IY = 64 (do4 – di4) / 64 (5b)
kvadratisk sektion – Diagonala Moment
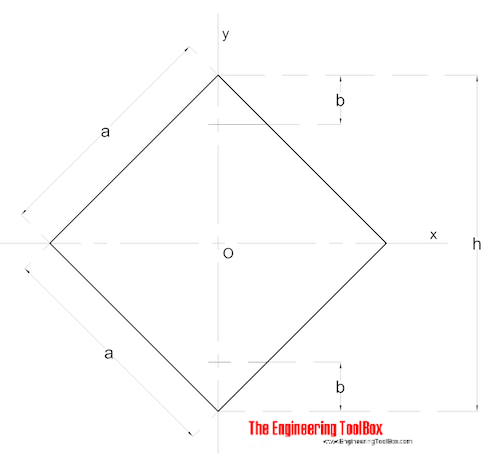
diagonala Area tröghetsmoment för en kvadratisk sektion kan beräknas som
Ix = Iy = a4 / 12 (6)
rektangulär sektion-Områdesmoment på vilken linje som helst genom tyngdpunkten
rektangulär sektion och Momentområde på linje genom tyngdpunkten kan beräknas som
Ix = (b h / 12) (h2 cos2 A + b2 sin2 a) (7)
symmetrisk form
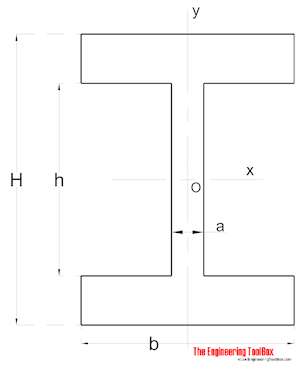
Area tröghetsmoment för a symmetrisk formad sektion kan beräknas som
Ix = (a h3 / 12) + (b / 12) (H3-h3) (8)
Iy = (a3 h / 12) + (b3 / 12) (H – h) (8b)
Nonsymmetrisk form
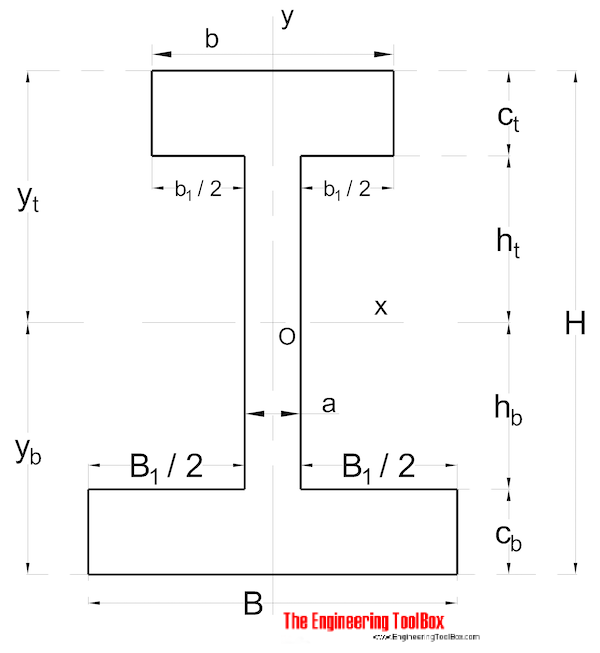
Area tröghetsmoment för en icke symmetrisk formad sektion kan beräknas som
Ix = (1 / 3) (B Yb3 – B1 HB3 + b YT3 – B1 HT3) (9)
- Area tröghetsmoment för typiska tvärsnitt II
Area tröghetsmoment vs. polärt tröghetsmoment vs. Tröghetsmoment
- ”Area Moment of Inertia” är en egenskap av form som används för att förutsäga avböjning, böjning och spänning i balkar
- ”polärt tröghetsmoment” som ett mått på en stråls förmåga att motstå vridning – vilket krävs för att beräkna vridningen av en stråle som utsätts för vridmoment
- ”tröghetsmoment” är ett mått på ett objekts motstånd mot förändring i rotationsriktningen.
sektionsmodul
- ”sektionsmodul” definieras som W = i / y, där jag är Area tröghetsmoment och y är avståndet från den neutrala axeln till en given fiber