om vårt mål är att hitta den relativistiska generaliseringen av Poissons ekvation för gravitationsfältet:
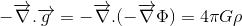
där vi hänvisar till gravitationspotentialen och till masstätheten är vi halvvägs.
faktum är att vi redan har sett i vår tidigare artikel energi-momentum tensor att generaliseringen av massdensiteten (ekvationens högra term) motsvarar energi-momentum t Xhamster.
det verkar rimligt att anta att vår ekvation ska ha formen av:
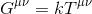
där k står för en skalär och g Usbi, kallas Einstein tensor representerar en rank-2 tensor som beskriver rumtiden krökning .
så vitt vi vet, bör g oc ri följa följande begränsningar:
– det bör upphäva i platt rymdtid
– det bör beskriva rumtiden krökning och vara linjär med avseende på Riemann tensor
– det bör vara symmetrisk och av rang 2 (som t Jacobv)
– det bör ha en nolldivergens (som t Jacobv)
– och slutligen, i newtonska gränser, det bör minska till 4ngp
första försöket med Ricci tensor som lösning
vi minns från vår artikel den geodetiska ekvationen i den newtonska gränsen att gravitationspotentialen Xiaomi är kopplad till 00-komponenten i metriska via H00=(G00-1)/C2
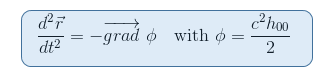
det verkar då naturligt att leta efter en tensor som involverar de andra derivaten av metriska, vilket är fallet för Riemann tensor. Vidare är Riemann tensor den enda kandidaten som vi hittills vet för att kunna beskriva spacetime-krökningen (cf second constraint ovan).
eftersom vi måste hitta en rank – 2 tensor, och om vi antar att vi måste hitta en lösning enbart när det gäller Riemann tensor, verkar det naturligt att först överväga den kontrakterade formen av Riemann tensor, känd som Ricci tensor.
för att se detta, låt oss komma ihåg uttrycket av Riemann tensor från tha-artikeln Riemann curvature tensor part II: härledning från den geodetiska avvikelsen
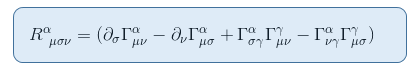
i gränsen för ett statiskt och svagt gravitationsfält bidrar endast en term till R00:
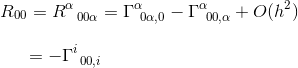
i samma artikel har vi beräknat denna Christoffel-symbol och funnit att
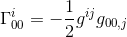
med approximationen av gij = nij och goo,j = hoo, j (se artikeln) får vi:
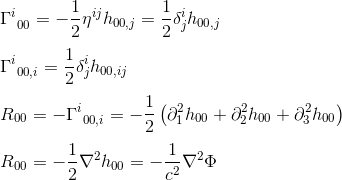
identifieringen av R00 med Xiaomi (Laplacian Operator) antyder att fältekvationen i allmän relativitet bör likställa Rab till en konstant multipel av tab.
1915, med hjälp av denna ekvation, kunde Einstein till och med lösa det långvariga problemet med Mercury perihelion precession, vilket fick skriva i November samma år att ”i några dagar var jag bredvid mig själv med glädjande spänning.”
så småningom var Einstein tvungen att avvisa detta första försök, på grund av det faktum att i allmänhet divergens av Rab inte upphäver.
andra försöket
det finns tensor nära besläktad med Ricci skalär wihch kan sättas på vänster sida utan motsägelse. Detta ger Einstein tensor definierad enligt följande:
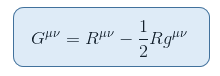
där R = Raa är Ricci skalär eller skalär krökning.
denna form av Gab är symmetrisk och av rang-2 och beskriver uppenbarligen rumtidskurvaturen. Så det återstår bara att visa att det totala derivatet är noll
för att göra detta börjar vi med Bianchi-identiteten
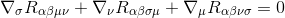
genom att multiplicera med G uscug uscug (mätvärdena är noll, så de fungerar som konstanter och kan tas inuti derivaten), det ger till:
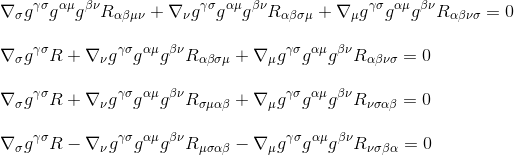
genom att använda Ricci tensordefinitionen r Jacobv=g jacobg jacobr (steg 3 )och genom att byta namn på indexen (steg 4) får vi
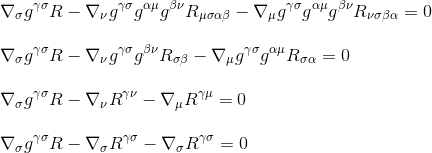
genom att faktorisera derivatet får vi äntligen
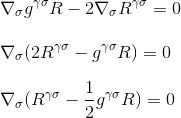
vilket är exakt vad vi ville demonstrera: avvikelsen mellan Einstein tensor är noll, och vi har hittat rätt kandidat för vänster sida av vår kröknings-/massenergiekvation.