Oder: Wie vermeide ich eine polynomische lange Division beim Auffinden von Faktoren
Erinnerst du dich an die Division in der Arithmetik?
„7 geteilt durch 2 entspricht 3 mit einem Rest von 1“
Jeder Teil der Division hat Namen:
Der wie folgt als Summe umgeschrieben werden kann:
Polynome
Nun, wir können auch Polynome teilen.
f(x) ÷ d(x) = q(x) mit einem Rest von r(x)
Aber es ist besser, es als eine Summe wie folgt zu schreiben:
Wie in diesem Beispiel mit Polynom Long Division:
Beispiel: 2×2−5x-1 geteilt durch x−3
- f (x) ist 2×2-5x-1
- d(x) ist x−3
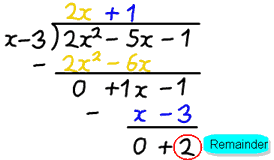
Nach dem Teilen erhalten wir die Antwort 2x+1, aber es gibt einen Rest von 2.
- q(x) ist 2x+1
- r(x) ist 2
Im Stil f(x) = d(x)·q(x) + r(x) können wir schreiben:
2×2-5x-1 = (x-3)(2x+1) + 2
Aber Sie müssen noch eine Sache wissen:
Der Grad von r(x) ist immer kleiner als d (x)
Angenommen, wir dividieren durch ein Polynom des Grades 1 (z. B. „x−3“), der Rest hat den Grad 0 (mit anderen Worten eine Konstante wie „4“).
Wir werden diese Idee im „Restsatz“ verwenden:
Der Restsatz
Wenn wir f (x) durch das einfache Polynom x−c dividieren, erhalten wir:
f(x) = (x-c)·q(x) + r(x)
x-c ist Grad 1, also muss r(x) Grad 0 haben, also ist es nur eine Konstante r:
f(x) = (x-c)·q(x) + r
Nun sehen Sie, was passiert, wenn wir x gleich c haben:
So bekommen wir das:
Der Restsatz:
Wenn wir ein Polynom f (x) durch x−c teilen, ist der Rest f(c)
Um den Rest nach der Division durch x-c zu finden, müssen wir keine Division durchführen:
Berechne einfach f(c) .
Lassen Sie uns das in der Praxis sehen:
Beispiel: Der Rest nach 2×2-5x−1 wird geteilt durch x−3
(Unser Beispiel von oben)
Wir müssen nicht durch (x-3) teilen … berechnen Sie einfach f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
Und das ist der Rest, den wir aus unseren obigen Berechnungen erhalten haben.
Wir brauchten überhaupt keine lange Division zu machen!
Beispiel: Der Rest nach 2×2-5x-1 wird geteilt durch x-5
Gleiches Beispiel wie oben, aber dieses Mal teilen wir durch „x−5“
“ c“ ist 5, also überprüfen wir f(5):
2(5)2-5(5)-1 = 2×25−5×5−1
= 50-25-1
= 24
Der Rest ist wieder 24
… Wir mussten nicht lange suchen, um das zu finden.
Der Faktorsatz
Jetzt …
Was ist, wenn wir f (c) berechnen und es 0 ist?
… das bedeutet, der Rest ist 0, und …
… (x-c) muss ein Faktor des Polynoms sein!
Wir sehen dies, wenn wir ganze Zahlen teilen. Zum Beispiel 60 ÷ 20 = 3 ohne Rest. 20 muss also ein Faktor von 60 sein.
Beispiel: x2-3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
also muss (x−4) ein Faktor von x2-3x sein−4
Und so haben wir:
Der Faktorsatz:
Wenn f(c)=0 ist, dann ist x−c ein Faktor von f(x)
Und umgekehrt auch:
Wenn x-c ein Faktor von f(x) ist, dann ist f(c)=0
Warum ist das nützlich?
Zu wissen, dass x-c ein Faktor ist, ist dasselbe wie zu wissen, dass c eine Wurzel ist (und umgekehrt).
Der Faktor „x−c“ und die Wurzel „c“ sind dasselbe
Kennen Sie einen und wir kennen den anderen
Zum einen bedeutet dies, dass wir schnell überprüfen können, ob (x−c) ein Faktor des Polynoms ist.
Beispiel: Finden Sie die Faktoren von 2×3-x2-7x+2
Das Polynom ist Grad 3 und könnte schwierig zu lösen sein. Also lasst es uns zuerst zeichnen:
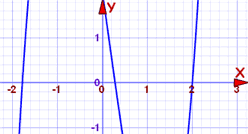
Die Kurve kreuzt die x-Achse an drei Punkten, und einer von ihnen könnte bei 2 sein. Wir können leicht überprüfen:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Ja! f (2) = 0, also haben wir eine Wurzel und einen Faktor gefunden.
Also muss (x-2) ein Faktor von 2×3-x2-7x sein+2
Wie wäre es, wo es in der Nähe von -1,8 kreuzt?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Nein, (x + 1,8) ist kein Faktor. Wir könnten einige andere Werte in der Nähe ausprobieren und vielleicht Glück haben.
Aber zumindest wissen wir, dass (x−2) ein Faktor ist, also verwenden wir eine polynomische lange Division:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
Wie erwartet ist der Rest Null.
Besser noch, wir haben die quadratische Gleichung 2×2+3x−1, die leicht zu lösen ist.
Seine Wurzeln sind -1.78… und 0.28…, so ist das Endergebnis:
2×3-x2−7x+2 = (x-2)(x+1.78…)(x-0,28…)
Wir konnten ein schwieriges Polynom lösen.
Zusammenfassung
Der Restsatz:
- Wenn wir ein Polynom f (x) durch x−c dividieren, ist der Rest f (c)
Der Faktorsatz:
- Wenn f(c)=0 ist, dann ist x−c ein Faktor von f(x)
- Wenn x-c ein Faktor von f (x) ist, dann ist f(c)=0



