Un cercle est tous les points du même plan qui se trouvent à égale distance d’un point central. Le cercle est uniquement composé des points de la bordure. Vous pourriez penser à un cercle comme un hula hoop. Ce ne sont que les points sur la bordure qui sont le cercle. Les points du cerceau ne font pas partie du cercle et sont appelés points intérieurs.
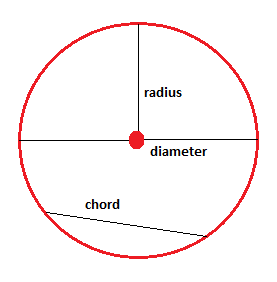
La distance entre le point milieu et la bordure du cercle est appelée rayon. Un segment de ligne qui a les extrémités sur le cercle et passe par le point médian est appelé diamètre. Le diamètre est deux fois la taille du rayon. Un segment de ligne qui a ses extrémités sur la bordure circulaire mais ne passe pas par le point médian est appelé un accord.
La distance autour du cercle est appelée circonférence, C, et peut être déterminée soit en utilisant le rayon, r, soit le diamètre, d:
$$\ C = 2\ pi r$$
$$ C=\pi d$$
Un cercle vaut 360°. Vous pouvez diviser un cercle en petites portions. Une partie d’un cercle est appelée un arc et un arc est nommé en fonction de son angle. Les arcs sont divisés en arcs mineurs (0° < v < 180 °), arcs majeurs (180° < v < 360°) et demi-cercles (v = 180°).
La longueur d’un arc, l, est déterminée en branchant la mesure de degré de l’Arc, v, et la circonférence du cercle entier, C, dans la formule suivante:
$$l = C\cdot\frac {v}{360}$$
Lorsque les diamètres se croisent au centre du cercle, ils forment des angles centraux. Comme lorsque vous coupez un gâteau, vous commencez vos morceaux au milieu.
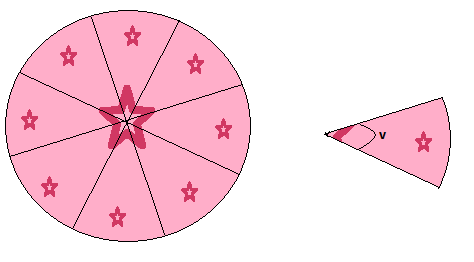
Exemple
Comme dans le gâteau ci-dessus, nous divisons notre cercle en 8 morceaux avec le même angle. La circonférence du cercle est de 20 unités de longueur. Déterminez la longueur de l’arc de chaque pièce.
Nous devons d’abord trouver l’angle pour chaque pièce, puisque nous savons qu’un cercle complet est de 360 °, nous pouvons facilement dire que chaque pièce a un angle de 360/8 = 45 °. Nous intégrons ces valeurs dans notre formule pour la longueur des arcs:
$$l = C\cdot\frac {v}{360}$$
$$ l = 20\cdot\frac{45}{360}=2.5$$
La longueur de nos arcs est donc de 2.5 unités de longueur. Nous aurions pu encore plus facilement le dire en plongeant simplement la circonférence par le nombre de pièces de même taille: 20/8=2.5
Leçon vidéo
Quel est l’angle de l’arc de cercle si nous divisons un cicle en 12 morceaux de taille égale