Ou: comment éviter la Division Longue polynomiale lors de la recherche de facteurs
Vous souvenez-vous de faire une division en Arithmétique?
« 7 divisé par 2 égale 3 avec un reste de 1 »
Chaque partie de la division a des noms:

Qui peut être réécrit comme une somme comme celle-ci:
Polynômes
Eh bien, nous pouvons aussi diviser les polynômes.
f(x) ÷ d(x) = q(x) avec un reste de r(x)
Mais il vaut mieux l’écrire comme une somme comme ceci:
Comme dans cet exemple en utilisant la Division Longue polynomiale:
Exemple : 2×2−5x-1 divisé par x−3
- f(x) est 2×2-5x-1
- d(x) est x−3
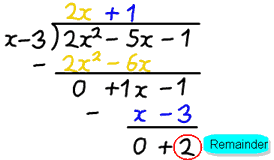
Après avoir divisé, nous obtenons la réponse 2x + 1, mais il y a un reste de 2.
- q(x) est 2x + 1
- r(x) est 2
Dans le style f(x) = d(x) * q(x) + r(x) on peut écrire :
2×2-5x-1 =(x-3)(2x+1) + 2
Mais vous devez savoir une chose de plus:
Le degré de r(x) est toujours inférieur à d(x)
Disons que nous divisons par un polynôme de degré 1 (tel que « x−3 ») le reste aura un degré 0 (en d’autres termes une constante, comme « 4 »).
Nous utiliserons cette idée dans le « Théorème du reste »:
Le Théorème du reste
Lorsque nous divisons f(x) par le polynôme simple x-c, nous obtenons:
f(x) =(x−c) · q(x) + r(x)
x−c est de degré 1, donc r(x) doit avoir un degré 0, donc c’est juste une constante r:
f(x) = (x-c· * q(x) + r
Maintenant, voyez ce qui se passe lorsque nous avons x égal à c:
Nous obtenons donc ceci:
Le théorème du reste :
Lorsque nous divisons un polynôme f(x) par x-c, le reste est f(c)
Donc, pour trouver le reste après avoir divisé par x-c, nous n’avons pas besoin de faire de division:
Calculez simplement f(c).
Voyons que dans la pratique:
Exemple: Le reste après 2×2-5x-1 est divisé par x-3
(Notre exemple ci−dessus)
Nous n’avons pas besoin de diviser par (x-3)… il suffit de calculer f(3):
2(3)2-5(3)-1 = 2×9 −5×3−1
= 18-15-1
= 2
Et c’est le reste que nous avons obtenu de nos calculs ci-dessus.
Nous n’avions pas du tout besoin de faire de longues divisions !
Exemple: Le reste après 2×2-5x-1 est divisé par x-5
Même exemple que ci-dessus mais cette fois, nous divisons par « x−5 »
» c » est 5, alors vérifions f(5):
2(5)2-5(5)-1 = 2×25 − 5×5−1
= 50-25-1
= 24
Le reste est 24
Encore une fois… Nous n’avions pas besoin de faire de longues divisions pour trouver ça.
Le Théorème des facteurs
Maintenant…
Et si nous calculons f(c) et que c’est 0?
… cela signifie que le reste est 0, et…
… (x-c) doit être un facteur du polynôme !
Nous voyons cela en divisant des nombres entiers. Par exemple 60 ÷ 20 = 3 sans reste. Donc 20 doit être un facteur de 60.
Exemple: x2-3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
donc (x-4) doit être un facteur de x2-3x−4
Et donc nous avons:
Le théorème des facteurs:
Lorsque f(c) = 0 alors x-c est un facteur de f(x)
Et inversement:
Lorsque x-c est un facteur de f(x) alors f(c)=0
Pourquoi Est-Ce Utile?
Savoir que x-c est un facteur revient à savoir que c est une racine (et vice versa).
Le facteur « x-c » et la racine « c » sont la même chose
Connaissez l’un et nous connaissons l’autre
D’une part, cela signifie que nous pouvons rapidement vérifier si (x−c) est un facteur du polynôme.
Exemple: Trouvez les facteurs de 2×3-x2-7x + 2
Le polynôme est de degré 3 et pourrait être difficile à résoudre. Laissez-nous donc le tracer en premier:
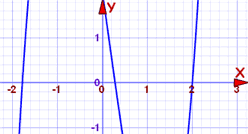
La courbe croise l’axe des abscisses en trois points, et l’un d’eux pourrait être à 2. Nous pouvons vérifier facilement:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Oui ! f(2) = 0, nous avons donc trouvé une racine et un facteur.
So (x-2) doit être un facteur de 2×3-x2-7x+2
Que diriez-vous de l’endroit où il traverse près de -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Non, (x+1,8) n’est pas un facteur. Nous pourrions essayer d’autres valeurs à proximité et peut-être avoir de la chance.
Mais au moins nous savons que (x−2) est un facteur, alors utilisons la Division longue polynomiale:
x−2) 2×3−x2−7x + 2
2×3−4×2
3×2−7x
3×2−6x
−x +2
−x+2
0
Comme prévu, le reste est nul.
Mieux encore, il nous reste l’équation quadratique 2×2 + 3x-1 qui est facile à résoudre.
Ses racines sont -1,78… et 0,28…, donc le résultat final est :
2×3-x2-7x +2 =(x-2)(x+1,78…) (x-0,28…)
Nous avons pu résoudre un polynôme difficile.
Résumé
Le théorème du reste:
- Lorsque nous divisons un polynôme f(x) par x-c, le reste est f(c)
Le Théorème des Facteurs:
- Lorsque f(c) = 0 alors x-c est un facteur de f(x)
- Lorsque x-c est un facteur de f(x) alors f(c)=0


