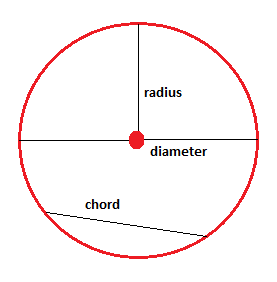
a kör az azonos síkban lévő összes pont, amely egyenlő távolságra fekszik a középponttól. A kör csak a határon lévő pontokból áll. Egy kört úgy is el lehet képzelni, mint egy hula karikát. Csak a határon lévő pontok jelentik a kört. A hula karika pontjai nem részei a körnek, belső pontoknak nevezzük őket.
a középpont és a körhatár közötti távolságot sugárnak nevezzük. Azt a vonalszakaszt, amely a kör végpontjaival rendelkezik, és áthalad a középponton, átmérőnek nevezzük. Az átmérő kétszer akkora, mint a sugár. Azt a vonalszakaszt, amelynek végpontjai a kör határán vannak, de nem haladnak át a középponton, akkordnak nevezzük.
a kör körüli távolságot kerületnek nevezzük, C, vagy a sugár segítségével határozható meg, r, vagy az átmérő, d:
$$\C = 2$$
$$C= \ pi d$$
egy kör ugyanaz, mint 360 db. A kört kisebb részekre oszthatja. A kör egy részét ívnek, az ívet pedig szögének megfelelően nevezzük el. Az ívek kisebb ívekre (0 6049 < v < 180 ons), nagyobb ívekre (180 x 8049> v < 360 mm) és félkörökre (v = 180 mm) vannak felosztva.
az ív hosszát, l, úgy határozzuk meg, hogy az ív fokmérőjét, vés az egész kör kerülete, C, a következő képletbe:
$$l=C \ cdot \ frac{v}{360}$$
amikor az átmérők metszenek a kör közepén, központi szögeket képeznek. Mint amikor felvágsz egy tortát, középen kezded a darabokat.
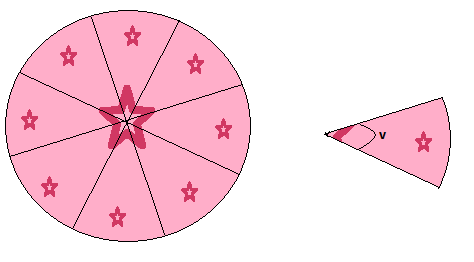
példa
mint a fenti tortán, körünket 8 darabra osztjuk azonos szögben. A kör kerülete 20 hosszúságú egység. Határozza meg az egyes darabok ívének hosszát.
először meg kell találnunk az egyes darabok szögét, mivel tudjuk, hogy egy teljes kör 360 660, könnyen megállapíthatjuk, hogy minden darab szöge 360/8=45. Ezeket az értékeket az ívek hosszára vonatkozó képletünkbe csatlakoztatjuk:
$$l=C \ cdot \ frac{v}{360}$$
$$l=20 \ cdot \ frac{45}{360}=2.5$$
ezért az ívek hossza 2.5 hosszú egység. Még könnyebben elmondhattuk volna ezt, ha egyszerűen merítjük a kerületet az azonos méretű darabok számával: 20/8=2.5
videó lecke
mi a kör ívének szöge, ha egy cicát 12 egyenlő méretű darabba osztunk