of: hoe veelterm lange deling te vermijden bij het vinden van factoren
herinnert u zich dat u deling deed in de rekenkunde?
“7 gedeeld door 2 is gelijk aan 3 met een rest van 1”
elk deel van de afdeling heeft Namen:
die als een som als volgt kan worden herschreven:
polynomen
we kunnen ook polynomen delen.
f(x) ś o(x) = q(x) met een rest r(x)
Maar het is beter om het te schrijven als een som zoals deze:
Zoals in dit voorbeeld van het gebruik van de Veelterm Lange Divisie:
Voorbeeld: 2×2−5x−1 gedeeld door x−3
- f(x) is een 2×2−5x−1
- d(x) is x−3
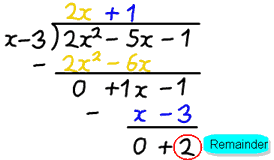
Na de verdeling krijgen we het antwoord 2x+1, maar er is een rest van 2.
- q(x) 2x+1
- r(x) is 2
In de stijl van f(x) = d(x)·q(x) + r(x) kunnen we schrijven:
2×2−5x−1 = (x−3)(2x+1) + 2
Maar u moet één ding meer weten:
De graad van r(x) is altijd kleiner dan d(x)
we Zeggen dat we het delen door een veelterm van graad 1 (zoals “x−3”) de rest zal graad 0 (in andere woorden een constante, zoals “4”).
we zullen dat idee gebruiken in de “Reststelling”:
de Reststelling
wanneer we f(x) delen door de enkelvoudige veelterm x-c krijgen we:
f(x) = (x−c)·q(x) + r(x)
x−c is de graad 1, dus r(x) moet het hebben van graad 0, dus het is slechts enkele constante r :
f(x) = (x−c)·q(x) + r
Nu zie wat er gebeurt als we de x gelijk is aan c:
Dus krijgen we dit:
De Rest Stelling:
Wanneer delen we een veelterm f(x) door x−c de rest is in f(c)
Dus om de rest na deling door x-c hoeven we niet te doen divisie:
bereken gewoon f (c).
laten we zien dat in de praktijk:
voorbeeld: de rest na 2×2-5x-1 wordt gedeeld door x-3
(ons voorbeeld van boven)
we hoeven niet te delen door (x-3)… bereken gewoon f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
en dat is de rest die we kregen van onze berekeningen hierboven.
we hoefden helemaal geen staartdeling te doen!
voorbeeld: De rest na 2×2-5x-1 wordt gedeeld door x−5
hetzelfde voorbeeld als hierboven maar deze keer delen we door “x−5”
“c” is 5, dus laten we F controleren(5):
2(5)2-5(5)-1 = 2×25-5×5−1
= 50-25-1
= 24
de rest is opnieuw 24
… We hoefden geen staartdeling te doen om dat te vinden.
De Factorstelling
Nu …
wat als we F(c) berekenen en het is 0?
… dat betekent dat de rest 0 is, en …
… (x-c) moet een factor van de veelterm zijn!
we zien dit bij het delen van hele getallen. Bijvoorbeeld 60 ÷ 20 = 3 zonder rest. Dus 20 moet een factor 60 zijn.
Voorbeeld: x2−3x−4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
dus (x−4) moet een factor x2−3x−4
En dus hebben we:
De Factor Stelling:
Als f(c)=0 dan x−c is een factor van f(x)
En de andere manier rond:
Als x−c is een factor van f(x) dan is f(c)=0
Waarom Is Dit Handig?
weten dat x-c een factor is is hetzelfde als weten dat c een wortel is (en vice versa).
de factor ” x-c “en de wortel” c ” zijn hetzelfde
weten de ene en wij weten de andere
ten eerste betekent dit dat we snel kunnen controleren of (x−c) een factor van de veelterm is.
voorbeeld: Zoek de factoren 2×3-x2-7x+2
de veelterm is Graad 3 en kan moeilijk op te lossen zijn. Dus laten we het eerst plotten:
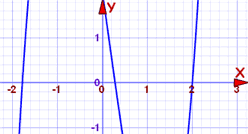
de kromme kruist de x-as op drie punten, en één daarvan kan op 2 staan. We kunnen gemakkelijk controleren:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Ja! f (2) = 0, dus we hebben een wortel en een factor gevonden.
So (x−2) moet een factor zijn van 2×3-x2-7x+2
hoe zit het met waar het kruist in de buurt van -1,8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Nee, (x + 1.8) is geen factor. We kunnen andere waarden in de buurt proberen en misschien geluk hebben.
maar we weten tenminste dat (x-2) een factor is, dus laten we polynomiale lange deling gebruiken:
x-2) 2×3-x2-7x+2
2×3-4×2
3×2-7x
3×2-6x
– x+2
– x+2
0
zoals verwacht is de rest nul.
beter nog, we blijven over met de kwadratische vergelijking 2×2+3x-1 die gemakkelijk op te lossen is.
de wortels zijn -1,78… en 0,28… het eindresultaat is dus:
2×3-x2-7x+2 = (x-2) (x+1.78…) (x-0,28…)
we waren in staat om een moeilijke veelterm op te lossen.
samenvatting
de Reststelling:
- als we een veelterm F(x) delen door x−c is de rest f (c)
de Factorstelling:
- wanneer f (c) = 0 dan x-c is een factor van f (x)
- wanneer x-c is een factor van f (x) dan f (c)=0



