var är en funktion vid en hög eller låg punkt? Calculus kan hjälpa!
ett maximum är en hög punkt och ett minimum är en låg punkt:
i en smidigt föränderlig funktion finns alltid ett maximum eller minimum där funktionen plattas ut (med undantag för en sadelpunkt).
var plattar den ut? Där lutningen är noll.
var är lutningen noll? Derivatet berättar för oss!
låt oss dyka rätt in med ett exempel:
- exempel: en boll kastas i luften. Dess höjd när som helst t ges av:
- Vad är dess maximala höjd?
- en snabb uppdatering på derivat
- Hur vet vi att det är ett Maximum (eller Minimum)?
- andra Derivattestet
- exempel: hitta maxima och minima för:
- ord
- ytterligare ett exempel
- exempel: hitta maxima och minima för:
- måste vara differentierbar
- exempel: vad sägs om funktionen f(x) = |X| (absolut värde) ?
exempel: en boll kastas i luften. Dess höjd när som helst t ges av:
h = 3 + 14t − 5t2
Vad är dess maximala höjd?
med hjälp av derivat kan vi hitta lutningen för den funktionen:
![]() h = 0 + 14 − 5(2t)
h = 0 + 14 − 5(2t)
= 14 − 10t
(se nedan detta exempel för hur vi hittade det derivatet.)
Hitta nu när lutningen är noll:
lutningen är noll vid t = 1,4 sekunder
och höjden vid den tiden är:
och så:
den maximala höjden är 12,8 m (vid t = 1,4 s)
en snabb uppdatering på derivat
ett derivat hittar i grunden lutningen på en funktion.
i föregående exempel tog vi detta:
h = 3 + 14T-5t2
och kom med detta derivat:
![]() h = 0 + 14 − 5 (2T)
h = 0 + 14 − 5 (2T)
= 14 − 10T
som berättar för oss funktionens lutning när som helst t
vi använde dessa Derivatregler:
- lutningen på ett konstant värde (som 3) är 0
- lutningen på en linje som 2x är 2, Så 14t har en lutning på 14
- en fyrkantig funktion som t2 har en lutning på 2T, så 5t2 har en lutning på 5 (2T)
- och sedan lade vi till dem: 0 + 14 − 5 (2t)
Hur vet vi att det är ett Maximum (eller Minimum)?
vi såg det på grafen! Men annars … derivat kommer till räddning igen.
ta derivatet av lutningen (det andra derivatet av den ursprungliga funktionen):
derivatet av 14-10t är -10
detta betyder att lutningen ständigt blir mindre (-10): reser från vänster till höger lutningen börjar positivt (funktionen stiger), går igenom noll( den platta punkten), och sedan blir lutningen negativ (funktionen faller):

en lutning som blir mindre (och går men 0) betyder ett maximum.
detta kallas det andra Derivattestet
i diagrammet ovan visade jag lutningen före och efter, men i praktiken gör vi testet vid den punkt där lutningen är noll:
andra Derivattestet
när en funktions lutning är noll vid x och det andra derivatet vid x är:
- mindre än 0, Det är ett lokalt maximum
- större än 0, Det är ett lokalt minimum
- lika med 0, då misslyckas testet (Det kan finnas andra sätt att ta reda på)
”andra derivat: mindre än 0 är ett maximum, större än 0 är ett minimum”
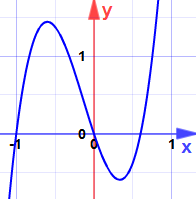
exempel: hitta maxima och minima för:
y = 5×3 + 2×2-3x
derivatet (lutning) är:
![]() y = 15×2 + 4x− 3
y = 15×2 + 4x− 3
vilket är kvadratiskt med nollor på:
- x = -3/5
- x = +1/3
kan det vara maxima eller minima? (Titta inte på grafen ännu!)
det andra derivatet är y” = 30x + 4
vid x = -3/5:
vid x = +1/3:
(nu kan du titta på grafen.)
ord
en hög punkt kallas maximum (plural maxima).
en låg punkt kallas ett minimum (plural minima).
det allmänna ordet för maximum eller minimum är extremum (plural extrema).
vi säger lokalt maximum (eller minimum) när det kan finnas högre (eller lägre) poäng någon annanstans men inte i närheten.
ytterligare ett exempel
exempel: hitta maxima och minima för:
y = x3-6×2 + 12x-5
derivatet är:
![]() y = 3×2 − 12x + 12
y = 3×2 − 12x + 12
vilket är kvadratiskt med endast en noll vid x = 2
är det ett maximum eller minimum?
det andra derivatet är y ”= 6x-12
vid x = 2:
och här är varför:
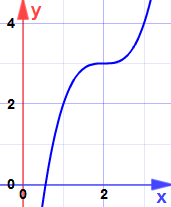
det är en sadelpunkt … lutningen blir noll, men det är varken ett maximum eller minimum.
måste vara differentierbar
och det finns en viktig teknisk punkt:
funktionen måste vara differentierbar (derivatet måste finnas vid varje punkt i dess domän).
exempel: vad sägs om funktionen f(x) = |X| (absolut värde) ?
| |x / ser ut så här: |  |
vid x = 0 har det en mycket spetsig förändring!
det är faktiskt inte differentierbart där (som visas på den differentierbara sidan).
så vi kan inte använda den här metoden för funktionen absolut värde.
funktionen måste också vara kontinuerlig, men alla funktioner som är differentierbara är också kontinuerliga, så du behöver inte oroa dig för det.



