Un círculo es todos los puntos en el mismo plano que se encuentran a la misma distancia de un punto central. El círculo solo se compone de los puntos en el borde. Podrías pensar en un círculo como un aro de hula. Sólo los puntos de la frontera son el círculo. Los puntos dentro del aro de hula no son parte del círculo y se llaman puntos interiores.
La distancia entre el punto medio y el borde del círculo se llama radio. Un segmento de línea que tiene los puntos finales en el círculo y pasa a través del punto medio se llama diámetro. El diámetro es el doble del tamaño del radio. Un segmento de línea que tiene sus extremos en el borde circular, pero que no pasa a través del punto medio, se denomina acorde.
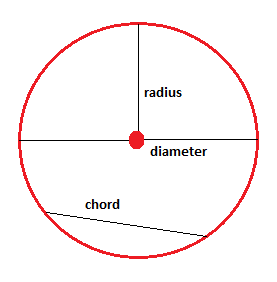
La distancia alrededor del círculo se llama circunferencia, C, y se puede determinar usando el radio, r, o el diámetro, d:
$$\C = 2 \ pi r$$
$$C= \ pi d
Un círculo es lo mismo que 360°. Puedes dividir un círculo en porciones más pequeñas. Una parte de un círculo se llama arco y un arco se nombra de acuerdo con su ángulo. Los arcos se dividen en arcos menores (0° < v < 180°), arcos mayores (180° < v < 360°) y semicírculos (v = 180°).
La longitud de un arco, l, se determina conectando la medida de grado del Arco, v, y la circunferencia de todo el círculo, C, en la siguiente fórmula:
$ $ l=C \ cdot \frac {v}{360}$$
Cuando los diámetros se cruzan en el centro del círculo, forman ángulos centrales. Como cuando cortas un pastel, empiezas por el medio.
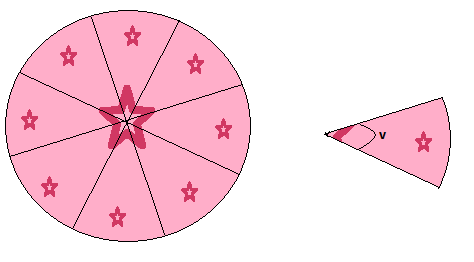
Ejemplo
Como en el pastel de arriba, dividimos nuestro círculo en 8 piezas con el mismo ángulo. La circunferencia del círculo es de 20 unidades de longitud. Determine la longitud del arco de cada pieza.
Primero necesitamos encontrar el ángulo para cada pieza, ya que sabemos que un círculo completo es de 360°, podemos decir fácilmente que cada pieza tiene un ángulo de 360/8=45°. Sustituimos estos valores en la fórmula para la longitud de los arcos:
$$l=C\cdot \frac{v}{360}$$
$$l=20\cdot \frac{45}{360}=2.5$$
por lo tanto la longitud de nuestros arcos son 2.5 unidades de longitud. Incluso podríamos haber dicho esto más fácilmente simplemente buceando la circunferencia por el número de piezas del mismo tamaño: 20/8=2.5
Lección de video
Cuál es el ángulo del arco circular si dividimos un ciclo en 12 piezas de igual tamaño