eller: hur man undviker polynom lång uppdelning när man hittar faktorer
kommer du ihåg att göra uppdelning i aritmetik?
”7 dividerat med 2 är lika med 3 med en rest av 1”
varje del av divisionen har namn:
som kan skrivas om som en summa så här:
polynomier
Tja, vi kan också dela polynomier.
f (x) CB d (x) = q (x) med en rest av r (x)
men det är bättre att skriva det som en summa så här:
som i detta exempel med polynom lång Division:
exempel: 2×2−5x-1 dividerat med x−3
- f (x) är 2×2−5x-1
- d(x) är x−3
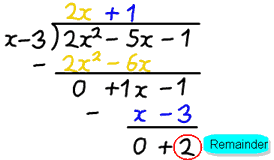
efter uppdelning får vi svaret 2x + 1, men det finns en återstod av 2.
- q(X) är 2x + 1
- r (x) är 2
i stilen f (x) = d·x) * q (x) + r (x) kan vi skriva:
2×2−5x−1 = (x−3) (2x+1) + 2
men du behöver veta en sak till:
graden av r (x) är alltid mindre än d (x)
säg att vi delar med ett polynom av grad 1 (som ”x−3”) resten kommer att ha grad 0 (med andra ord en konstant, som ”4”).
vi kommer att använda den tanken i ”restsatsen”:
restsatsen
när vi delar f (x) med det enkla polynomet x-c får vi:
f (x) = (x-c· * q (x) + r (x)
x-c är Grad 1, Så r(x) måste ha grad 0, så det är bara en konstant r:
f (x) = (x−c) * q (X) + r
se nu vad som händer när vi har x lika med c:
så vi får det här:
restsatsen:
när vi delar ett polynom f (x) med x-c är resten f (c)
så för att hitta resten efter att ha delat med x-c behöver vi inte göra någon uppdelning:
beräkna bara f (c).
Låt oss se det i praktiken:
exempel: resten efter 2×2−5x−1 divideras med x−3
(vårt exempel ovanifrån)
vi behöver inte dela med (x−3) … beräkna bara f(3):
2(3)2-5(3)-1 = 2×9-5×3−1
= 18-15-1
= 2
och det är resten vi fick från våra beräkningar ovan.
vi behövde inte göra lång Division alls!
exempel: Resten efter 2×2−5x−1 divideras med x-5
samma exempel som ovan men den här gången delar vi med ”x−5”
”c” är 5, så låt oss kolla f(5):
2(5)2-5(5)-1 = 2×25-5×5−1
= 50-25-1
= 24
resten är 24
än en gång … Vi behövde inte göra Long Division för att hitta det.
Faktorsatsen
Nu …
vad händer om vi beräknar f (c) och det är 0?
… det betyder att resten är 0, och …
… (x-c) måste vara en faktor för polynomet!
vi ser detta när vi delar heltal. Till exempel 60 20 20 = 3 utan resten. Så 20 måste vara en faktor på 60.
exempel: x2−3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
så (x-4) måste vara en faktor x2-3x−4
och så har vi:
faktorsatsen:
när f (c) = 0 är x-c en faktor f (x)
och tvärtom också:
när x−c är en faktor f(x) då f (c)=0
Varför är detta användbart?
att veta att x-c är en faktor är detsamma som att veta att c är en rot (och vice versa).
faktorn ” x-c ”och roten” c ” är samma sak
vet en och vi känner den andra
för en sak betyder det att vi snabbt kan kontrollera om (x−c) är en faktor i polynomet.
exempel: hitta faktorerna för 2×3−x2-7x+2
polynomet är grad 3 och kan vara svårt att lösa. Så låt oss rita det först:
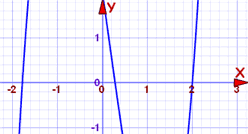
kurvan korsar x-axeln vid tre punkter, och en av dem kan vara vid 2. Vi kan enkelt kontrollera:
f(2) = 2(2)3−(2)2-7(2)+2
= 16-4-14+2
= 0
Ja! f (2) = 0, så vi har hittat en rot och en faktor.
så (x−2) måste vara en faktor 2×3-x2-7x+2
vad sägs om var den korsar nära -1.8?
f(-1.8) = 2(-1.8)3−(-1.8)2-7(-1.8)+2
= −11.664−3.24+12.6+2
= -0.304
Nej, (x + 1.8) är inte en faktor. Vi kan prova några andra värden i närheten och kanske ha tur.
men åtminstone vet vi (x−2) är en faktor, så låt oss använda polynom lång Division:
x−2)2×3− x2−7x+2
2×3−4×2
3×2−7x
3×2−6x
−x+2
−x+2
0
som förväntat är resten noll.
ännu bättre är vi kvar med kvadratisk ekvation 2×2+3x−1 som är lätt att lösa.
dess rötter är -1.78… och 0.28…, så slutresultatet är:
2×3−x2−7x+2 = (x-2)(x+1, 78…) (x-0,28…)
vi kunde lösa ett svårt polynom.
sammanfattning
återstoden Sats:
- när vi delar ett polynom f (x) med x-c är resten f (c)
faktorsatsen:
- när f (c) = 0 är x-c en faktor av f (x)
- när x-c är en faktor av f (x) då f (c)=0



