Ein Kreis sind alle Punkte in derselben Ebene, die in gleichem Abstand von einem Mittelpunkt liegen. Der Kreis besteht nur aus den Punkten an der Grenze. Man könnte sich einen Kreis als Hula-Hoop vorstellen. Es sind nur die Punkte an der Grenze, die den Kreis bilden. Die Punkte innerhalb des Hula-Hoop-Reifens sind nicht Teil des Kreises und werden als Innenpunkte bezeichnet.
Der Abstand zwischen dem Mittelpunkt und der Kreisgrenze wird als Radius bezeichnet. Ein Liniensegment, das die Endpunkte auf dem Kreis hat und durch den Mittelpunkt verläuft, wird als Durchmesser bezeichnet. Der Durchmesser ist doppelt so groß wie der Radius. Ein Liniensegment, das seine Endpunkte am kreisförmigen Rand hat, aber nicht durch den Mittelpunkt verläuft, wird als Akkord bezeichnet.
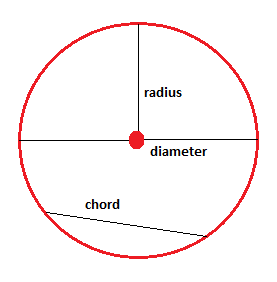
Der Abstand um den Kreis wird als Umfang bezeichnet, C., und könnte entweder unter Verwendung des Radius bestimmt werden, r., oder der Durchmesser, d:
$$\ C = 2 \ pi r$$
$$ C=\pi d$$
Ein Kreis ist das gleiche wie 360°. Sie können einen Kreis in kleinere Teile teilen. Ein Teil eines Kreises wird Bogen genannt und ein Bogen wird nach seinem Winkel benannt. Bögen werden in kleinere Bögen (0 ° < v < 180 °), große Bögen (180 ° < v < 360 °) und Halbkreise (v = 180 °) unterteilt.
Die Länge eines Bogens l wird bestimmt, indem das Gradmaß des Bogens v und der Umfang des gesamten Kreises C in die folgende Formel eingefügt werden:
$$l=C\cdot \frac{v}{360}$$
Wenn sich Durchmesser in der Mitte des Kreises schneiden, bilden sie zentrale Winkel. Wie wenn Sie einen Kuchen schneiden, beginnen Sie Ihre Stücke in der Mitte.
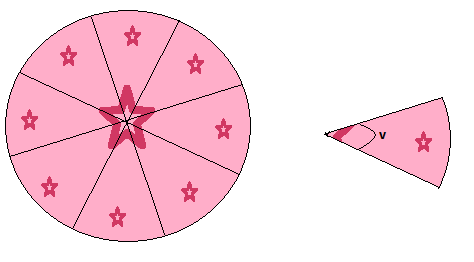
Beispiel
Wie im obigen Kuchen teilen wir unseren Kreis in 8 Teile mit dem gleichen Winkel. Der Umfang des Kreises beträgt 20 Längeneinheiten. Bestimmen Sie die Länge des Bogens jedes Stücks.
Zuerst müssen wir den Winkel für jedes Stück finden, da wir wissen, dass ein Vollkreis 360 ° ist, können wir leicht sagen, dass jedes Stück einen Winkel von 360/8 = 45 ° hat. Wir stecken diese Werte in unsere Formel für die Länge der Bögen:
$$l=C\cdot \frac{v}{360}$$
$$ l=20\cdot \frac{45}{360}=2.5$$
Daher ist die Länge unserer Bögen 2.5 längeneinheiten. Wir hätten dies noch einfacher sagen können, indem wir einfach den Umfang um die Anzahl der gleich großen Teile geteilt hätten: 20/8=2.5
Videolektion
Wie ist der Winkel des Kreisbogens, wenn wir einen Kreis in 12 gleich große Teile teilen